Machine Shop Maths

Linear Equations

The above video lesson is part of a series of videos I made for Practical Machinist, available here

The subject of linear transposition of equations comes up in college when we are studying for our machining qualifications. Often, the lecturers explain the subject like it is a refresher course. For most of us, it is a whole new concept that we never expected to have to learn to be a machinist or that it is essential knowledge to work in a machine shop. If you zoned out at school and never got a grasp of this subject. I explain it in easy-to-follow terms with examples below in this video I made for Practical Machinist.

Let's look at how linear equations work:

Finding the value of x

Let's start nice and simple and say 2x=10. The 2x means two times an unknown value.

This 'x' is also known as a variable. When macro programming on our CNC machines we need to work with variables all the time, so understanding how we can manipulate them is important when writing probing cycles and various macro programs.

So we know that this equation means 2 times an unknown value is equal to 10. This can only be one thing because the only number that can be multiplied by 2 that will equal 10 is 5.

In this example, 'x' our unknown variable is equal to 5.

We can see what these equations would be but it gets much more complicated when we have an unknown on both sides of the equals. That's what we are going to discuss in this article.

Linear equation with 2 or more unknowns

$Linear equation with 2 or more unknowns$

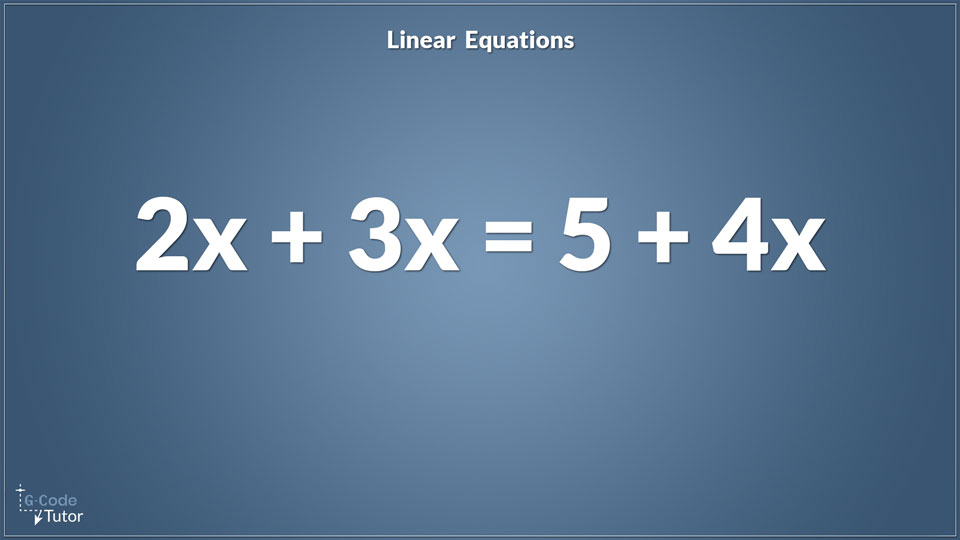
Let's start with 2x again but this time we're going to say:

2x + 3x = 5 + 4x

We can't see the answer this time as it doesn't jump out at us so we are going to need to solve it using maths.

To solve it let's start with 2x + 3X. This is the same as saying 5x. We don't need to add the X's together we just add the number that's multiplied by the x. So the equation now looks like this:

5x = 5 + 4x

The next step is to get all those x's on one side of the equal sign. To do that we need to remove that 4x from the right-hand side of the equation and pop it over to the other side to make this problem easy to solve. We do that just by taking away the 4x from the right side of the equation. What we do to one side of the equation we have to do to the other. So if we minus 4x from the right-hand side we also have to minus 4x from the left side. Our equation now looks like this:

5x - 4x = 5

Now the answer is within our reach, if we do the sum on the left of the equals sign, 5x - 4x we are left with 1x. also written as x.

x = 5

Now we can see that x is equal to 5

Still confused? watch the video above for a step-by-step process and more examples.

Share this article